Writing Linear Equations Using Slope and Point
Given two points (x1, y1) and (x2, y2) FIND the value for m, then USE the values for m,
and either point as ( x1, y1 ) as the replacement values in the equation:
y = m(x – x1) + y1 then solve for y = m x + b.
1. Find the slope, y-intercept and write the equation of the line that passes through the points (3, 2)
and (6, – 2).
Given points: (3, 2), (6, - 2) Find dy and dx directly from the table or the points.
substitute these in the equation y = m(x – x1) + y1 and simplify to y = m x + b.
or
Thus, b = 6
Write:
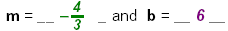
Equation:
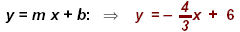
Check:
Write the equation given two points:
2. Given (2, -1) and (- 3, 2) plot the points and draw the line through the points and write the
equation for the line.
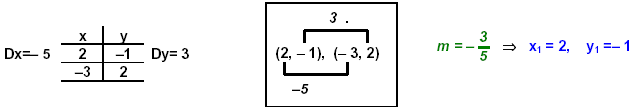
Using the point (2, –1). write the values:
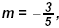 , x1
= 2, and y1 = –1 as replacements in the equation:
substitute these in the equation y = m(x – x1) + y1 and simplify to y = m x + b.
or
Thus, b = 6
Write:
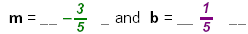
Equation:
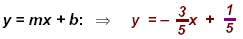
Check: Use the other point ( –3, 2): Replace the x and y in the equation with x = –3 and y = 2.
in the equation that you found above. If you get a true statement then your work is correct.
Show work here:
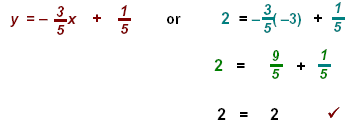
3. Given points: (3, 2), (5, –3) Find Dy and Dx directly from the table or the points.
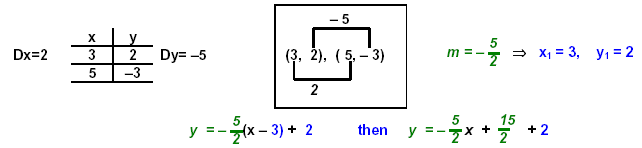
Write:
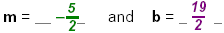
Equation:
|
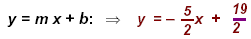
