Subtracting Fractions
Expressed in symbols, the rule for subtracting one fraction
from another is as follows:
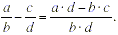
Let’s break this down to see everything that is expressed
in this rule. The numerator of the sum is a · d - b · c . This
is almost exactly the same as the pattern of cross-multiplying .
The only difference is that because the fractions are subtracted,
a minus sign now joins the a · d to the b · c .
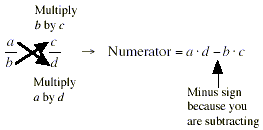
To get the denominator of the sum, you just multiply the two
denominators ( b and d ) together.
Example
Work out each of the following differences of fractions.
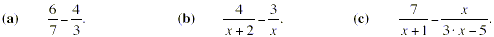
Solution
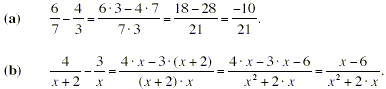
In the numerator, the “3” multiplies the entire
quantity ( x + 2) to give 3 · x + 6. Note that the “ -
” sign in the numerator applies to both the 3 · x and the
+6, giving - 3 · x - 6 in the numerator, not - 3 · x + 6.
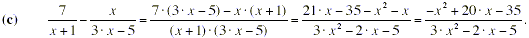
As in the previous example, note that the “ - ” that
appears in from of the x · ( x + 1) in the numerator applies to
both the x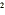 and the x that are generated when x · ( x
+ 1) is multiplied out. This gives the - x
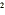- x that appears in the numerator, not 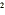- x+
x .
|
