Solving Equations
Solving Equations with ther Variable on Both Sides
To solve an equation that has the variable on both sides, use
the properties of equality to write an equivalent equation that
has the variable on only one side. Then solve. When you solve
equations that contain grouping symbols, you may need to use the
distributive property to remove the grouping symbols. Some
equations may have no solution because there is no value of the
variable that will result in a true equation. For example, x + 1
= x + 2 has no solution; it cannot be true. An equation that is
true for every value of the variable is called an identity . For
example, x + x = 2 x is true for every value of x.
Example
Solve 3( x - 2) = 4 x + 5.
Solution
First use the distributive property to remove the parentheses.
3x - 6 = 4x + 5
Next, collect all the terms with x on one side of the equal
sign by subtracting 3x from each side.
3x - 6 - 3x = 4x + 5 - 3x
| - 6 = x + 5 |
Add like terms. |
| - 6 - 5 = x + 5 - 5 |
Subtract 5 from each side. |
| - 11 = x |
|
Solving Equations and Formulas
Some equations contain more than one variable. To solve an
equation or formula for a specific variable, you need to get that
variable by itself on one side of the equation.
When you divide by a variable in an equation, remember that
division by 0 is undefined. When you use a formula, you may need
to use dimensional analysis, which is the process of carrying
units throughout a computation.
Example
Solve the formula d = rt for t .
Solution
The variable t has been multiplied by r, so divide each side
by r to isolate t.
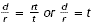
Thus 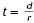 , where r , where r 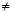 0.
0.
|