Slopes of Perpendicular Lines
Perpendicular lines intersect at a right angle.
If two nonvertical lines are perpendicular, then their slopes are negative
reciprocals of each other.
That is, if the slope of one line is
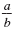 , then the slope of any perpendicular
line is , then the slope of any perpendicular
line is
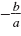 . .
| The product of the slopes of two
perpendicular lines is -1. |
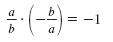 |
Note: To find the negative reciprocal of a
fraction, switch the numerator and the
denominator and change the sign.
For example, the negative reciprocal of
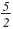 is is
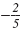 . The negative reciprocal of
-3 is . The negative reciprocal of
-3 is
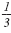 . .
Example 1
Find the slope of a line perpendicular to the line that passes through the
points (-4, 1) and (1, -2).
Solution
First, find the slope of the line through the given points.
| Let (x1, y1) = (-4, 1) and (x2, y2)
= (1, 2). |
m |
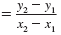 |
| Substitute the values in the slope formula.
|
|
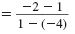 |
| Simplify. |
|
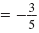 |
The slope of the line through
(-4, 1) and (1, -2) is
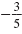 . .
The negative reciprocal of
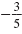 is is
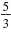 . .
A line perpendicular to the line through (-4, 1) and (1, -2) has slope
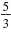 . .
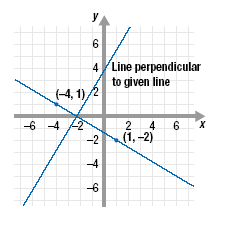
Example 2
Determine if line A is perpendicular to line B.
Solution
The slopes,
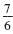 and and
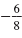 , are not negative reciprocals so the lines are
not perpendicular. , are not negative reciprocals so the lines are
not perpendicular.
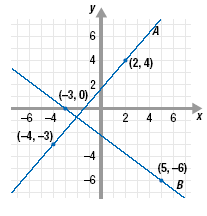
Be careful! The lines do look
perpendicular. But the relationship
between their slopes tells us the lines are
not perpendicular.
|