Inverse Functions
Sometimes one function can "undo" what another function does. For example, consider f(x)
= 5x over the
domain {1, 2, 3}
1 → 5
2 → 10
3 → 15
Now consider
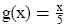 over the domain {5, 10, 15} over the domain {5, 10, 15}
5 → 1
10 → 2
15 → 3
Note: f takes 2 to 10, and g takes 10 back to 2.
This is an example of a pair of functions that are inverses of each other.
Before we officially define inverses, we need another definition...
One-to-One Function:
A one-to-one function has exactly one output for each input and exactly one input
for each output. This means that in addition to the fact that no two points can have the same first coordinate,
in order to be a one-to-one function, it must also be true that no two points can have the same second
coordinate. Graphically, we can use the Horizontal Line Test to determine if a function is one-to-one.
Horizontal Line Test: A function is one-to-one if no horizontal line intersects its graph in more than one
point.
Now, back to inverses. It is true that every one-to-one function has an inverse. Now we are ready to
define inverse functions.
DEFINITION: Functions f and g for which f(g(x)) = x and g(f(x)) = x for all x in the domains of
f and g are called inverse functions. We denote the inverse of f by f-1, read "f
inverse".
Our next question is: "How do we go about finding the inverse of a one-to-one function?" There is a four
step process for finding a function inverse.
Finding the Inverse of a Function
To find the inverse of a one-to-one function defined by the equation y = f(x):
1. Rewrite the equation, replacing f(x) with y.
2. Interchange x and y.
3. Solve the resulting equation for y. (If this equation cannot be solved uniquely for y, the original
function has no inverse.)
4. Replace y with f-1(x).
Verifying That Two Functions Are Inverses
To verify that two functions are inverses, you must show that both of the following are true:
f(f-1(x)) = x and f-1(f(x)) = x
The domain of a function will become the range of its inverse and the range of a function will become the
domain of its inverse.
|