Factoring by Grouping
Factoring:
Some rules governing factoring in elementary algebra:
1. The numbers (coefficients) must be real and rational.
2. The powers must be whole numbers.
3. Prime factors include:
a) Linear polynomial, such as (x + 3), (x + y + z)
b) The sum of an even degree term (2 or higher) with any real number, such as:
(x2 + 4), (x2 y2 + 9), (2x2 + 25), (x2
+ 3), etc.
c) The sum of two even-powered terms, such as: (x4 + y4), (x6 + y8), (x2 + y6)
d) Certain quadratic trinomials which cannot be expressed as the product of two linear
binomials with rational numbers. There is a special test for this which will be discussed
later.
Factor Quadratic Polynomials:
|
WHAT TO DO: |
HOW TO DO IT: |
| 1. First, examine the polynomial to see if it has a
common factor(s) in each term. Integers as
common factors are left in composite form and
letters are left in power form. Note the remaining
factor is prime. |
a) 3x2 + 12
3(x2 + 4) prime factors
b) 5x3 + 7x2
x2(5x + 7) prime factors |
| Factor out that common factor(s) and see what is
left. If the remaining polynomial is prime*, leave
the factors “as isâ€.
|
c) 3x3 − 21x2 + 27x
3x(x2 − 7x + 9) prime factors |
| If the inner polynomial is factorable, set it aside
to examine separately and come back to complete. |
d) 4x2 − 12x − 8x + 24
4(x2 − 3x − 2x + 6) |
| 2. Consider the inner polynomial: x2 − 3x − 2x + 6
grouped 2×2 by underlining the first two and last two.
Factor common factor from each group.
Bring down middle sign.
Complete factoring |
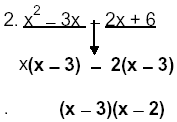 |
| Now, go back to the original problem and write
the answer in completely factored form. |
d) 4x2 − 20x + 24
4(x2 − 5x + 6)
4(x − 3)(x − 2) |
|