nth Roots
Now we will study higher order roots, such as cube roots. Like square
roots, these roots can be written using a radical symbol. To indicate the
specific root, a number called the index is written just above the
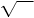 on
the radical symbol. on
the radical symbol.
For example, the cube root of 8 is written like this:
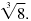 The index, 3, indicates the radical is a cube root. The index, 3, indicates the radical is a cube root.
The cube root of 8 is 2 because 23 = 8. We write:
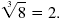
Note:
The square root of a number is also called
the 2nd root of the number. The index of a square root is 2, but we
rarely write it. Thus,
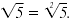
The cube root of a number is also called the 3rd root of the number.
In a similar way, we define 4th roots, 5th roots, 6th roots, and so on. For example,
• The 4th root of 81 is written like this:
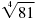 . The index is 4. . The index is 4.
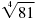 = 3 because 34 = 81.
= 3 because 34 = 81.
• The 10th root of 1 is written like this:
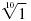 . The index is 10. . The index is 10.
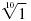 = 1 because 110 = 1.
= 1 because 110 = 1.
To indicate an nth root, we use the letter n for the index.
• If n is odd, then
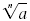 is always a real number. is always a real number.
For example,
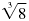 and and
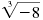 are both real numbers: are both real numbers:
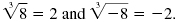
• If n is even, then
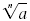 is a real number only when a
≥ 0. is a real number only when a
≥ 0.
For example,
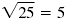 , but , but
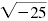 is not a real number because
5 · 5 ≠
-25 and (-5) · (-5)
≠ -25. is not a real number because
5 · 5 ≠
-25 and (-5) · (-5)
≠ -25.
In fact, no real number
multiplied by itself will equal -25.
| n |
nth root |
symbol |
| 2 |
square root |
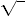 |
| 3 |
cube root |
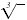 |
| 4 |
fourth root |
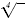 |
| 5 |
fifth root |
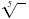 |
 |
 |
 |
Example
a. Find
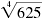 b. Find the 5th root of 243. b. Find the 5th root of 243.
Solution
a. Find the prime factorization of 625: 625 = 5 · 5
· 5 · 5 = 54 . Since 54 = 625, and 5 is positive,
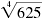 = 5.
= 5.
b. The 5th root of 243 may be written
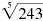 . Find the prime factorization of
243: 243 = 3 · 3
· 3 · 3
· 3 = 35. Since 35 = 243, . Find the prime factorization of
243: 243 = 3 · 3
· 3 · 3
· 3 = 35. Since 35 = 243,
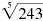 = 3.
= 3.
|