Rounding Numbers
Question: What is 14 489 to the nearest 1000?
Misconception
To obtain the answer, round to the
nearest 10, 100 and then 1000; thus:
14 489 to the nearest 10 is 14 490,
14 490 to the nearest 100 is 14 500,
14 500 to the nearest 1000 is 15 000.
Hence: the misconception leads to the incorrect
answer, 15 000.
|
Correct
The answer must be either 14 000 or 15 000, and since
14 489 - 14 000 = 489,
whilst
15000 - 14 489 = 511,
clearly 14 489 is nearer to 14 000 than to 15 000.
Hence: the correct answer is 14 000.
|
Further Explanation
The correct explanation above, that 14 489 is nearer to 14 000
than to 15 000, is clear-cut; but why is the 'misconceived'
method wrong?
This is best illustrated by taking another example and putting
it into context.
Two stations, A and B, are 500 metres apart:
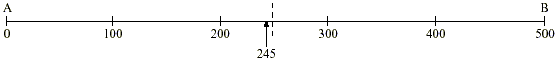
You stand between the stations, 245 m away from A and 255 m
from B and you want to walk to the nearest station. Naturally you
turn left and walk 245 m.
But now imagine there are five trains parked between the
stations, each train 100 m long, and each divided into 4
carriages of equal length.
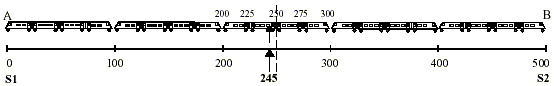
Your position, 245 m away from A, is now 20 m along the second
carriage of the third train, and you decide to find your way to
the nearest station by first asking which is the nearest
carriage-end (the one on the right, 250 metres from A). Having
moved there, you then seek the nearest end of the train , which
(as, by convention, we round mid-points up) is to the right at
300 metres from A. From there finally, you go to the nearest
station , and this time arrive at B.
Clearly the result is wrong. Why?
Because when you want to find the nearest station , the
questions about the nearest carriageend and the nearest train end
are irrelevant. Doing it this way might not matter in some cases,
but here it does. The unnecessary interim steps move you away
from your starting point, and here, in the wrong direction.
Another instructive point: this exercise provides an opportunity
to distinguish between an arbitrary convention (i.e. which way to
go from the middle) and a reasoned choice (i.e. the correct
approach to round).
|