Solving Trigonometric Equations
How would you solve the equation sin θ = 0?
You know that θ = 0 is one solution,
but this is not the only solution. Any one of the following values of is also a
solution.
..., -3π, -2π, -π, 0, π, 2π, 3π,...
You can write this infinite solution set as {nπ:
n is an integer}
Example 1
Solving a Trigonometric Equation
Solve the equation
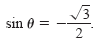
Solution
To solve the equation, you should consider that the sine is negative in
Quadrants III and IV and that
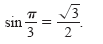
Thus, you are seeking values of θ in the third and fourth quadrants that have a reference
angle of π/3. In the interval
[0, 2π], the two angles fitting these criteria are
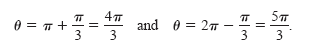
By adding integer multiples of 2π to each of these solutions, you obtain the following
general solution.
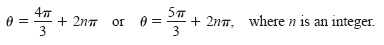
See the figure below.
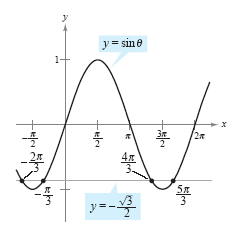
Solution points of
Example 2
Solving a Trigonometric Equation
Solve cos 2θ = 2 - 3 sin θ, where 0
≤ θ ≤ 2π.
Solution
Using the double-angle identity cos 2θ = 1 - 2
sin2θ, you can rewrite the
equation as follows.
| cos 2θ
|
= 2 - 3 sin θ |
Given equation |
| 1 - 2 sin2θ |
= 2 - 3 sin θ |
Trigonometric identity |
| 0 |
= 2sin2θ - 3sin θ
+ 1 |
Quadratic form |
| 0 |
= (2 sin θ)(sin
θ - 1) |
Factor. |
If 2 sin θ = 0, then sin
θ = 1/2 and θ =
π/6 or θ = 5π/6. If sin θ - 1, then
sin θ = 1 and θ
= π/2. Thus, for 0 ≤ θ ≤ 2π, there are three solutions.
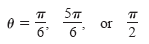
|