Linear Equations
Graphing Linear Equations
| Graphing Equations Using Two
Points |
Use the equation to find the coordinates
of any two points on the line. Draw the line representing
the equation by connecting them. The two points chosen
can be the x- and y-intercepts. |
| Graphing Equations Using a Point
and the Slope |
Graph one point and use the slope to find
another point by moving the distance of the change in y
and then the distance of the change in x from that point.
When the equation is in point-slope form, y - y1
= m( x - x1), use the point ( x1, y1)
and the slope m. When the equation is in slope-intercept
form, y = mx + b, use the point (0, b) and the slope m. |
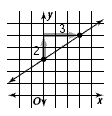
Example
Graph -2x + 3y = 9 by using the slope and y -intercept.
Solution
| 3y = 2x + 9 |
Solve the equation for y. |
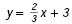 |
Slope-intercept form. |
y-intercept: 3 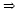 |
(0, 3) is on the line. |
slope of line: 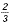 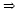 |
Move up 2 units, then right 3 units from
that point. |
Parallel and Perpendicular Lines
| Parallel Lines |
Lines in the same plane that never
intersect are called parallel lines. If two nonvertical
lines have the same slope, then they are parallel. All
vertical lines are parallel. |
| Perpendicular Lines |
Lines that intersect at right angles are
called perpendicular lines. If the product of the slopes
of two lines is -1, then the lines are perpendicular. The
slopes of two perpendicular lines are negative
reciprocals of each other. In a plane, vertical lines and
horizontal lines are perpendicular. |
Example
Determine whether the graphs of 2 y = -3 x + 4 and 3 y = 2 x -
9 are parallel, perpendicular, or neither.
Solution
Rewrite each line in slope-intercept form to identify its
slope.
| 2 y = -3 x + |
3 y = 2 x - 9 |
 |
 |
Since 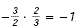 , these lines are perpendicular. , these lines are perpendicular.
Midpoint of a Line Segment
| Midpoint of a Line Segment |
The midpoint of a line segment is the
point that is halfway between the endpoints of the
segment. The coordinates of the midpoint of a line
segment whose endpoints are at ( x1, y1)
and ( x2, y2) are given by 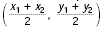 |
Example
The midpoint of a segment is M (2, 3) and one endpoint is B (
-1, 5). Find the coordinates of the other endpoint.
Solution
Let M(2, 3) = (x, y) and B( -1, 5) = ( x1, y1).
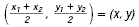
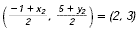
Form two equations by setting the x-coordinates equal to each
other and the y-coordinates equal to each other.
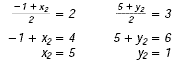
Coordinates of the other endpoint: (5, 1).
|