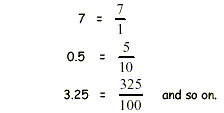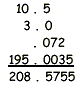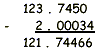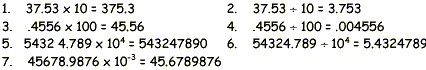Decimals

A decimal is a number that can be written as a fraction whose denominator is 1, 10, 100, 1000, and so on. For example: Decimal Notation = Fraction Notation

In a whole number, the decimal point is located to the right of the digit in the ones place. For example: (252 = 252 .). The place value of a digit is determined by where it is in relation to the decimal point. The digits to the left of the decimal point are whole numbers; they have place values of 1, 10, 100, 1000, 10,000 and so on. The digits to the right of the decimal point are fractional parts; they have place values of and so on. Note: each place is as large as the place to its immediate left.

In the place value chart, the numbers to the left of the decimal point end in ‘s’ and represent the whole number part of the decimal while the numbers to the right of the decimal point end in ‘ths’ and represent the fractional part of the decimal.

To write the word name for a Decimal: If there is no number other than ‘0’ to the left of the decimal point, omit steps one and two.

1. Write the name for the whole number to the left of the decimal point.
2. Write the word ‘and’ for the decimal point.
3. Write the name for the number to the right of the decimal point as if it were a whole number. Then write the name for the place value of the last digit on the right.

Example: 253.5674 is two hundred fifty-three and five thousand six hundred seventy-four ten- thousandths.

To add or subtract decimals, line up all the decimal points in a vertical column.

Example 1. add: 10.5 + 3 +.072 + 195.0035

Example 2. Subtract: 123.7450 – 2.00034

To multiply two decimals:

1. Multiply the two numbers as if they were whole numbers.
2. Locate the decimal point by counting the number of decimal places (to the right of the decimal point) in both numbers. The total of these two counts is the number of decimal places the product must have.
3. If necessary, add zeros to the left of the numeral so that there are enough decimal places.

Examples:

1. 2.7 x 4 = 10.8 Notice that there is ‘1’ decimal place in the product.

2. 3.456 x .5 = 1.7280 In this product, there are ‘4’ decimal places. 1.7280 can also be written as 1.728.

3. .45 x .12 Notice that 45 x 12 = 540, but there should be 4 decimal places in the product. Therefore, add a zero to the left of the ‘5’.

.45 x .12 = .0540 = .054

To divide two decimal numbers:

1. If the divisor is not a whole number, move both decimal points to the right the same number of decimal places until the divisor is a whole number.
2. Place the decimal point in the quotient above the decimal place in the dividend.
3. Divide as if both numbers were whole numbers.
4. If the numbers do not divide evenly, round off to the given place value.

Examples:

Multiplication and Division by powers of Ten: A power of ten is a number that can be written as a product of tens; 10, 100, 1000, 10000…..are powers of ten. In exponential form, these are A power of ten can be recognized by looking for the number ten written with an exponent or a single ‘1’ followed by zeros.

To multiply a number by a power of ten, move the decimal point to the right. To divide a number by a power of ten, move the decimal point to the left. The number of places to move is shown by the number of zeros in the power of ten. If the exponent of ten is negative, move the decimal point to the left as in division.

Examples: