Fractions
Introduction
The ability to work confidently with fractions, both number
fractions and algebraic fractions, is an essential skill which
underpins all other algebraic processes. In this leaflet we
remind you of how number fractions are simplified, added,
subtracted, multiplied and divided.
1. Expressing a fraction in its simplest form
In any fraction 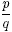 , say, the number p at the top is called
the numerator. The number q at the bottom is called the
denominator. The number q must never be zero. A fraction can
always be expressed in different, yet equivalent forms. For
example, the two fractions , say, the number p at the top is called
the numerator. The number q at the bottom is called the
denominator. The number q must never be zero. A fraction can
always be expressed in different, yet equivalent forms. For
example, the two fractions 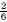 and and 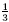 are equivalent. They represent the same
value. A fraction is expressed in its simplest form by cancelling
any factors which are common to both the numerator and the
denominator. You need to remember that factors are numbers which
are multiplied together. We note that are equivalent. They represent the same
value. A fraction is expressed in its simplest form by cancelling
any factors which are common to both the numerator and the
denominator. You need to remember that factors are numbers which
are multiplied together. We note that
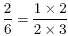
and so there is a factor of 2 which is common to both the
numerator and the denominator. This common factor can be
cancelled to leave the equivalent fraction 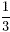 .
Cancelling is equivalent to dividing the top and the bottom by
the common factor. .
Cancelling is equivalent to dividing the top and the bottom by
the common factor.
Example
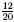 is equivalent to
is equivalent to 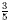 since since
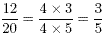
2. Addition and subtraction of fractions
To add two fractions we first re-write each fraction so that
they both have the same denominator. This denominator is chosen
to be the lowest common denominator. The is the smallest number
which is a multiple of both denominators. Then, the numerators
only are added, and the result is divided by the lowest common
denominator.
Example
Simplify
a) 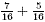
b) 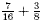
Solution
a) In this case the denominators of each fraction are already
the same. The lowest common denominator is 16. We perform the
addition by simply adding the numerators and dividing the result
by the lowest common denominator. So, 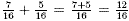 . This
answer can be expressed in the simpler form . This
answer can be expressed in the simpler form 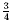 by
cancelling the common factor 4. by
cancelling the common factor 4.
b) To add these fractions we must rewrite them so that they
have the same denominator. The lowest common denominator is 16
because this is the smallest number which is a multiple of both
denominators. Note that 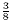 is equivalent to is equivalent to 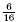 and so
we write and so
we write 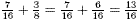 . .
Example
Find 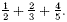
Solution
The smallest number which is a multiple of the given
denominators is 30. We express each fraction with a denominator
of 30.
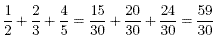
3. Multiplication and division of fractions
Multiplication of fractions is more straightforward. We simply
multiply the numerators to give a new numerator, and multiply the
denominators to give a new denominator. For example
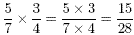
Division is performed by inverting the second fraction and
then multiplying. So,
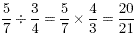
|