Adding and Subtracting Fractions
Adding and Subtracting Fractions with the Same Denominator
PROCEDURE: To add fractions with the same
denominator, add the numerators and put the sum over the original
denominator. To subtract fractions with the same denominator,
subtract the numerators and put the difference over the original
denominator.
SAMPLE PROBLEM A:
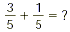
Add the numerators, and put the sum over the original
denominator:
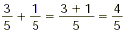
SAMPLE PROBLEM B:
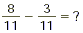
Subtract the numerators and put the difference over the
original denominator:
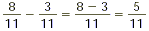
Adding and Subtracting Fractions with Different Denominators
Sometimes you have to add or subtract fractions that have
different denominators. To do this, you first need to rewrite
your fractions so that they DO have the same denominator.
Figuring out the least common denominator (LCD) of your fractions
is the first step.
PROCEDURE: To find the least common
denominator of two fractions, find the least common multiple of
the denominators. In other words, look at the multiples of the
numbers, and find out which they have in common. The common
multiple with the lowest value is your LCD.
SAMPLE PROBLEM:
What is the LCD of 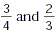 ? ?
Step 1: List the multiples of 4.
(4 × 1) × 4, (4 × 2) × 8, (4 × 3) × 12,
(4 × 4) × 16, etc.
Step 2: List the multiples of 3.
(3 × 1) × 3, (3 × 2) × 6, (3 × 3) × 9, (3 × 4) × 12,
etc.
The least common denominator of 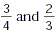 is 12. is 12.
Putting the LCD to Work
Now that you know how to find the LCD, you are all set to add
and subtract fractions with different denominators. Follow the
steps below to see how to use the LCD to add and subtract
fractions with different denominators.
PROCEDURE: To add or subtract fractions with
different denominators, first find the LCD of the two fractions.
Then determine the factor that each denominator is of that LCD.
Multiply both the numerator and the denominator by those factors
so that the fractions have the same denominator. Then add or
subtract the numerators.
SAMPLE PROBLEM:
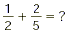
Step 1: Find the LCD.
(2 × 1) × 2, (2 × 2) × 4, (2 × 3) × 6, (2 × 4) × 8, (2
× 5) × 10, etc.
(5 × 1) × 5, (5 × 2) × 10, etc.
The LCD is 10 .
Step 2: Determine the factor that each
denominator is of the LCD.
Because 2 × 5 × 10, 5 is the factor of 2 .
Because 5 × 2 × 10, 2 is the factor of 5 .
Step 3: Multiply the factors of the LCD by
the fractions.
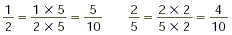
Step 4: Add the fractions.
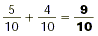
|