Rational Numbers
A rational number is a number that can be expressed in the
form 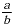 , where a and b are integers and b is not equal to 0. , where a and b are integers and b is not equal to 0.
| Comparing Rational
Numbers
|
If the graph of a is to the left of the
graph of b on a number line, then a < b. For any
two numbers a and b, exactly one of these is true:
a < b, a = b, a > b
You can use cross products to compare two fractions.
For rational numbers 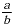 and and 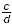 , with b >0 and d > 0, , with b >0 and d > 0,
- if
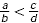 , then ad < bc, and , then ad < bc, and
- if ad < bc, then
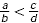 . .
|
Example
Use a calculator to write the fractions 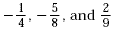 as decimals. Then order the fractions from least to greatest.
as decimals. Then order the fractions from least to greatest.
Solution
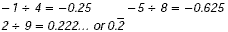
The decimals from least to greatest are 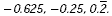 So
the fractions should be ordered So
the fractions should be ordered 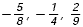 . .
Adding and Subtracting Rational Numbers
To add or subtract rational numbers, use the same rules you
used to add integers. When you are adding three or more rational
numbers, you can use the commutative and associative properties
to rearrange the addends.
Example
Find 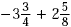 . .
Solution
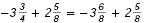 The LCD is 8. The LCD is 8.
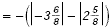 The sum is negative. The sum is negative.
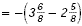
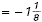 Subtract absolute values. Subtract absolute values.
Multiplying Rational Numbers
The product of two numbers having the same sign is positive.
The product of two numbers having different signs is negative. It
is also useful to note that multiplying a number or expression by
-1 results in the opposite of the number or expression. This is
called the multiplicative property of -1.
Example
Evaluate 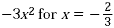
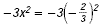 |
Replace x with 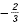 |
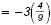 |
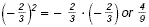 |
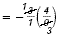 |
Divide out common factors. |
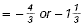 |
Multiply. The signs are different, so the
product is negative. |
Dividing Rational Numbers
You can use the same rules of signs when dividing rational
numbers that you used for multiplying.
| Dividing Two Rational Numbers |
The quotient of two numbers having the
same sign is positive. The quotient of two numbers
having different signs is negative.
|
If a fraction has one or more fractions in the numerator or
denominator, it is a complex fraction. To simplify a complex
fraction, rewrite it as a division expression.
Example
Simplify 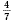
Solution
Rewrite the complex fraction as 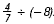
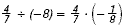 |
Multiply by 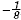 the reciprocal of -8. the reciprocal of -8. |
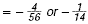 |
The signs are different, so the product is negative. |
|