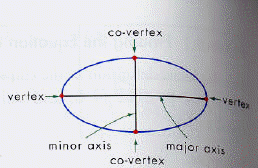
The Ellipse
An ellipse is the set of points P in the plane such that the sum of the
distances from P to two fixed points F1 and F 2 is a
constant.
F1P + F 2P = k the points F1 & F 2
the foci.
Using the idea of the two stacked cones, the ellipse is made when an angled
vertical cut is made

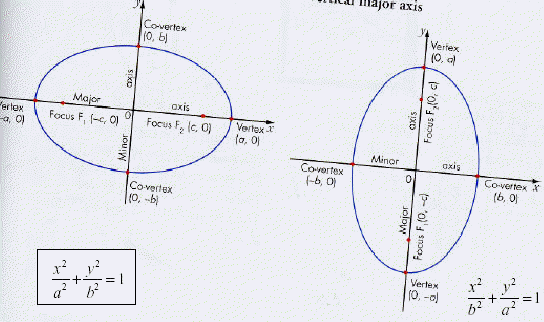
The important characteristics of the ellipse:
Example 1
Given 4x 2 + y 2 = 36 , find the equation of the
ellipse and give the coordinates of the foci.
Solution:
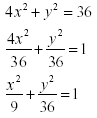
The foci
Given the equation, we see the major axis is along the y axis, and is centred
at the origin.
This means the vertices are at (0, -6) & (0,6), with co- vertices at (-3,0) &
(3,0).
| a 2 |
= b 2 + c 2 |
| 36 - 9 |
= c 2 |
| 27 |
= c 2 |
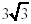 |
= c |
Hence the foci are at (0,
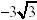 ) and (0, ) and (0,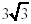 ) )
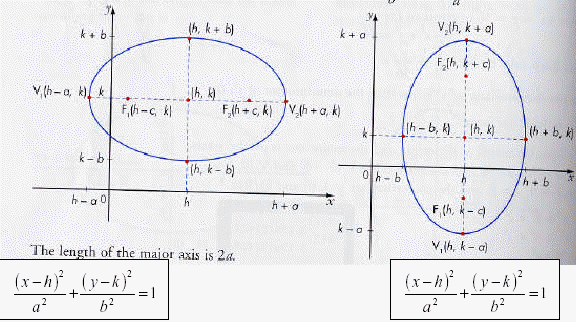
Ellipse are often not centered at the origin: Hence the possible ellipses are
Sketch
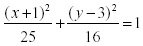 , and label the
foci , and label the
foci
We can from the equation that the major axis is parallel to the x axis.
The length of the major axis is 2a, which is 10. the minor axis is 2b, which is
8.
The vertices are (h - a , k) & (h + a, k), which are going to give ( -6, 3) &
(4, 3).
The co-vertices are (h, k - b) & ( h, k + b), which are going to give (-1, -1) &
(-1, 7).
The foci are going to be (h - c, k) & ( h + c, k)
Where c is equal to
| a 2 |
= b 2 + c 2 |
| c 2 |
= 25 - 16 |
| c |
= 3 |
Hence the foci are ( -4, 3 ) & ( 2, 3 )
Write the equation of an ellipse in standard form given:
· The centre is at (2,-1).
· The major axis is 16 units and is parallel to the x axis.
· The minor axis is 4 units.
Solution:
The centre is at (2,-1), with h = 2 & k = -1.
If the length of the major axis is 16, and the major axis is 2a, then
16 = 2a
a = 8
The length of the minor axis is 2.
Since we know h, k, a ,b we can solve the equation.
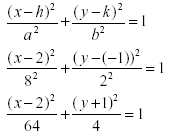
|