Rational Exponents
We can also use exponential notation to represent a radical. To do so, we
use a rational exponent.
Recall that a rational number is a number that may be written as the ratio
of two integers.
So, a rational exponent may be a fraction, such as
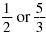 , or an integer
such as , or an integer
such as
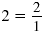 . .
Definition — Rational Exponent With Numerator 1
If a is a real number, then
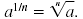
Here, n is a positive integer.
If n is odd, then a1/n is a real number.
If n is even, then a1/n is a real number only when a
≥ 0.
Using this definition, we write:
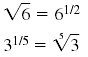
Note:
The way we interpret 2n depends upon
the value of n:
• n is a whole number
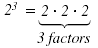
• n is zero
20 = 1
• n is a negative integer
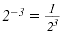
• n is a fraction
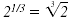
Example
Rewrite using a radical and evaluate: 1251/3
Solution
| Write the radical symbol.
|
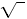 |
The index is 3, the denominator of the exponent
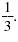 |
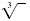 |
| The radicand is 125, the base of the exponential expression.
|
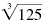 |
Find the prime factorization of 125.
125 = 5 · 5
· 5 = 53.
Since 53 = 125, the cube root of 125 is 5.
So,
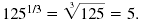
|