Relatively Prime Numbers
What is Relatively Prime?
Relatively prime is a term that is seemingly misleading. The
number 15 is relatively prime to 16, but neither 15 nor 16 is
prime. By definition, two numbers are relatively prime if and
only if the greatest common divisor of both numbers is 1. The
most common type of problem found on number sense tests involving
relatively prime numbers is “How many positive numbers less
than or equal to x are relatively prime to x ?”
Number of positive numbers less than x Relatively Prime to x
To find the number of positive numbers less than x that are
relatively prime to x , follow these steps:
- Find the prime factorization of x in the form of
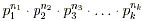 where p i is a unique
prime factor of x and n i is the power of
prime p i found in x . where p i is a unique
prime factor of x and n i is the power of
prime p i found in x .
- Then for each prime number pi ; (1
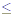 i i 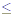 k ), create two new numbers Ai
and Bi . Ai = pi - 1 and k ), create two new numbers Ai
and Bi . Ai = pi - 1 and
 . Finally, the number of positive
integers less than or equal to x and relatively prime to
x is determined by finding the product of all Ai
· Bi ; (1 . Finally, the number of positive
integers less than or equal to x and relatively prime to
x is determined by finding the product of all Ai
· Bi ; (1 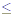 i i 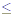 k ). The following following is a
generalization. k ). The following following is a
generalization.
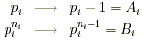
So, in other words, if x = 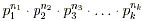 , then the number of positive numbers less than or
equal to x that are relatively prime to x is , then the number of positive numbers less than or
equal to x that are relatively prime to x is
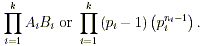
So,... what does that mean?
Without all the scary math symbols, here’s basically what
you have to do:
For each prime factor raised to some power, find the number
one less than the prime and the number that is the prime raised
to a power that is one less than the original power.
I think some examples will be helpful.
Example:
How many positive numbers less than or equal to 15 are
relatively prime to 15?
First, factor 15 into its primes: 15 = 3 1 · 5
1
Then, use the formula above:
For 3 1 , we get 3 - 1 = 2 and 3 1 - 1 =
3 0 = 1 (Every positive number raised to the zero
power is 1.)
Also from 5 1 , we get 5 - 1 = 4 and 5 1 - 1
= 5 0 = 1.
Multiply all the new numbers together to get the answer. 2 ×
1 × 4 × 1 = 8.
This example was easy because every prime has a power of 1.
When this is the case, you can simply multiply the numbers one
less than the primes to find the number of positive integers less
than x that are relatively prime.
Example:
How many positive numbers less than or equal to 16 are
relatively prime to 16?
First, factor 16 into its primes: 16 = 2 4
Then, use the formula:
For 2 4 , we get 2 - 1 = 1 and 2 4 - 1 =
2 3 = 8.
Multiply these two numbers together to get the answer. 1 × 8
= 8.
Example:
How many positive numbers less than or equal to 144 are
relatively prime to 144?
Factor 144 = 2 4 × 3 2 .
Use the formula for each prime:
From 2 4 , we get 2 - 1 = 1 and 2 4 - 1
= 2 3 = 8.
From 3 2 , we get 3 - 1 = 2 and 3 2 - 1
= 3 1 = 3.
Multiply these numbers together to get the answer. 1 × 8 × 2
× 3 = 48.
|