Solving Linear Systems of Equations by Elimination
Helpful Strategies When Using Elimination
Different linear systems may require different strategies for eliminating
one of the variables.
1. In some linear systems, a variable can be eliminated simply by adding
the equations.
| Add the equations to eliminate y.
There is no need to multiply
either equation by a constant. |
|
4x -x |
- + |
3y 3y |
= = |
- |
19 16 |
|
3x |
+ |
0y |
= |
- |
3 |
|
2. In a system that contains fractions, multiply both sides of an equation
by the LCD of its fractions to clear the fractions and make the system
easier to work with.
3. In some systems, only one equation needs to be multiplied by a
constant.
| Eliminate x. |
5x - 7y
15x + 8y |
= -33
=17 |
| Multiply both sides of the first equation by -3. Do not
change the second equation.
Add the equations to eliminate x |
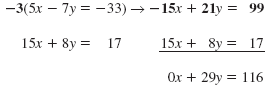 |
The solution of the system is (-1, 4).
4. In some systems, both equations must be multiplied by a constant.
| Eliminate x. |
-2x + 11y 3x - 5y |
= -28
= 19 |
| Multiply both sides of the first equation by 3. Multiply both sides of the second equation by 2.
Add the equations to eliminate x. |
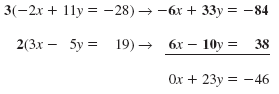 |
The solution of the system is (3, -2).
|