The Distance and Midpoint Formulas
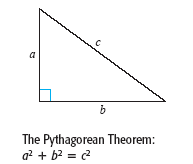
Recall from the Pythagorean Theorem that, in a right triangle, the hypotenuse c and
sides a and b are related by a2 + b2 = c2. Conversely, if
a2 + b2 = c2, the triangle is
a right triangle (see the figure below).
Suppose you want to determine the distance d between the two points (x1,
y1) and (x2, y2)
in the plane. If the points lie on a horizontal line, then y1 = y2 and the distance
between the points is | x2 - x1
|. If the points lie on a vertical line, then
x1 = x2 and the
distance between the points is | y2
- y1 |. If the two points do not lie on a horizontal or
vertical line, they can be used to form a right triangle, as shown in the figure
below.
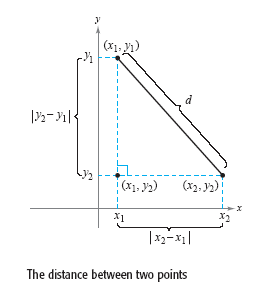
The
length of the vertical side of the triangle is |
y2 - y1 | and the length of the horizontal
side is | x2 - x1
|. By the Pythagorean Theorem, it follows that
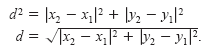
Replacing | x2 - x1
| 2 and
|y2 - y1
| 2 by the equivalent expressions
(x2 - x1)
2 and (y2 - y1)
2 produces the following result.
Distance Formula
The distance d between the points (x1, y1) and (x2,
y2) in the plane is given by
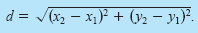
Example 1
Finding the Distance Between Two Points
Find the distance between the points (-2, 1) and (3, 4).
Solution
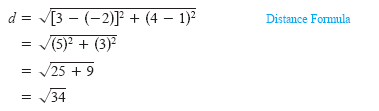
Example 2
Verifying a Right Triangle
Verify that the points (2, 1), (4, 0), and (5, 7) form the vertices of a right triangle.
Solution
The figure below shows the triangle formed by the three points.
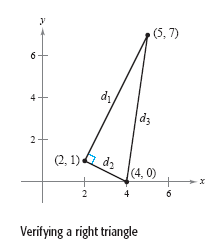
The lengths of
the three sides are as follows.
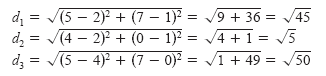
Because
| d12 + d22 = 45
+ 5 = 50 |
Sum of squares of sides |
and
| d32 = 50 |
Square of hypotenuse |
you can apply the Pythagorean Theorem to conclude that the triangle is a right
triangle.
Example 3
Using the Distance Formula
Find x such that the distance between (x, 3) and (2, -1) is 5.
Solution
Using the Distance Formula, you can write the following.
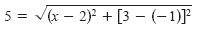 |
Distance Formula
|
| 25 = (x2 - 4x + 4) + 16 |
Square both sides.
|
| 0 = x2 - 4x - 5 |
Write in standard form. |
| 0 = (x - 5)(x + 1) |
Factor. |
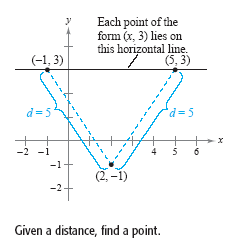
Therefore, x = 5 or x = -1, and you can conclude that there are two solutions. That
is, each of the points (5, 3) and (-1, 3) lies five units from the point as shown
in the following figure.
The coordinates of the midpoint of the line segment joining two points can be
found by “averaging†the x-coordinates of the two points and “averaging†the y-coordinates
of the two points. That is, the midpoint of the line segment joining the points
(x1, y1) and (x2, y2) in the plane is
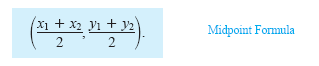
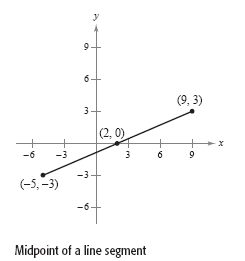
For instance, the midpoint of the line segment joining the points (-5, -3) and
(9, 3)
is
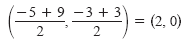
as shown in the figure below
|