Factoring Trinomials with Leading Coefficient 1
Let’s look closely at an example of finding the product of two binomials using the
distributive property:
| (x + 3)(x + 4) |
= (x + 3)x + (x + 3)4 |
Distributive property |
| |
= x2 + 3x + 4x + 12 |
Distributive property |
| |
= x2 + 7x + 12 |
|
To factor x2 + 7x + 12, we need to reverse these steps. First observe that the coef-
ficient 7 is the sum of two numbers that have a product of 12. The only numbers that
have a product of 12 and a sum of 7 are 3 and 4. So write 7x as 3x + 4x:
x2 + 7x + 12 = x2 + 3x + 4x+ 12
Now factor the common factor x out of the first two terms and the common factor 4
out of the last two terms. This method is called factoring by grouping.
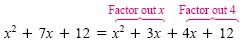 |
Rewrite 7x as 3x + 4x. |
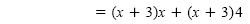 |
Factor out common factors. |
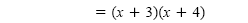 |
Factor out the common factor x + 3. |
Example 1
Factoring a trinomial by grouping
Factor each trinomial by grouping.
a) x2 + 9x + 18
b) x2 - 2x - 24
Solution
a) We need to find two integers with a product of 18 and a sum of 9. For a product
of 18 we could use 1 and 18, 2 and 9, or 3 and 6. Only 3 and 6 have a sum of 9.
So we replace 9x with 3x � 6x and factor by grouping:
| x2 + 9x + 18 |
= x2 + 3x + 6x + 18 |
Replace 9x by 3x + 6x. |
| |
= (x + 3)x + (x + 3)6 |
Factor out common factors. |
| |
= (x + 3)(x + 6) |
Check by using FOIL. |
b) We need to find two integers with a product of -24 and a sum of -2. For a product
of 24 we have 1 and 24, 2 and 12, 3 and 8, or 4 and 6. To get a product of -24
and a sum of -2, we must use 4 and -6:
| x2 - 2x - 24 |
= x2 - 6x + 4x - 24 |
Replace -2x with -6x + 4x. |
| |
= (x - 6)x + (x - 6)4 |
Factor out common factors. |
| |
= (x - 6)(x + 4) |
Check by using FOIL. |
The method shown in Example 1 can be shortened greatly. Once we discover
that 3 and 6 have a product of 18 and a sum of 9, we can simply write
x2 + 9x + 18 = (x + 3)(x + 6).
Once we discover that 4 and -6 have a product of -24 and a sum of -2, we can
simply write
x2 - 2x - 24 = (x - 6)(x + 4).
In the next example we use this shortcut.
Example 2
Factoring ax2 + bx + c with a = 1
Factor each quadratic polynomial.
a) x2 + 4x + 3
b) x2 + 3x - 10
c) a2 - 5a + 6
Solution
a) Two integers with a product of 3 and a sum of 4 are 1 and 3:
x2 + 4x + 3 = (x + 1)(x + 3)
Check by using FOIL.
b) Two integers with a product of 10 and a sum of 3 are 5 and -2:
x2 + 3x - 10 = (x + 5)(x - 2)
Check by using FOIL.
c) Two integers with a product of 6 and a sum of -5 are -3 and -2:
a2 - 5a + 6 = (a - 3)(a - 2)
Check by using FOIL.
|