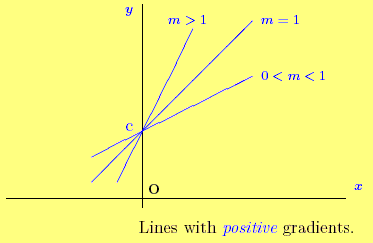
Straight Lines

Positive and Negative Gradients

If a line has gradient m = 1 then, providing that the scales are the same for both axes, it makes an angle of 45º with the positive x-axis. If m > 1 then the gradient is steeper. If 0 < m < 1 then the line makes an angle between 0º and 45º with the positive x-axis.

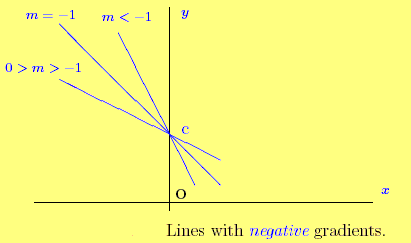
The diagram below illustrates lines similar to those of the previous diagram except with negative gradients. They are the mirror images of thestraight lines which are shown in the previous diagram, with the y axis actingas the mirror.

Exercise 1

In each of the following either the coordinates of twopoints, P,Q are given, or the coordinates of a single point R and agradient m . In each case, find the equation of the line.

(a) P (1 , 1) , Q (2 , - 1)

(b) R (1 , 2) , m = 2

(c) P ( - 1 , 2) , Q (1 , - 3)

(d) R ( - 2 , 1) , m = 4

Solutions

(a) Let the line be y = mx + c . Since both P (1 , 1) andQ (2 , - 1) lie on the line, both sets of coordinates must satisfy theequation. Thus we have

1 = m × 1 + c using the coordinates of P

- 1 = m × 2 + c using the coordinates of Q

or m + c = 12 m + c = - 1 .

This is a set of simultaneous equations which can be solved to givem = - 2 and c = 3 .

The required equation is thus

y = - 2 x + 3 .

Substituting the coordinates for P and then Q into this equation will confirm that this line passes through both of these points.

(b) Since m = 2 , the equation must have the form y =2 x + c and only the value of c remains to be found. The line passesthrough R (1 , 2) so the coordinates of this point must satisfy the equation. Thus

y = 2 x + c

2 = 2 × 1 + c using the coordinates of R

giving c = 0 .

The equation of the line is now

y = 2 x .

(c) Let the line be y = mx + c . Since both P ( - 1 , 2) and Q (1 , - 3) lie on the line, both sets of coordinates must satisfy theequation. Thus we have

2 = m × ( - 1 ) + c using the coordinates of P

- 3 = m × 1 + c using the coordinates of Q

or - m + c = 2m + c = - 3 .

This is a set of simultaneous equations which can be solved to givem = - 5 / 2 and c = - 1 / 2 .

The required equation isthus

y = - 52 x - 12 .

Substituting the coordinates for P and then Q into this equation will confirm that this line passes through both of these points.

(d) Since m = 4 , the equation must have the form y =4 x + c and only c remains to be found. The line passes throughR ( - 2 , 1) so the coordinates of this point must satisfy the equation. Thus

y = 4 x + c

1 = 4 × ( - 2) + c using the coordinates of R

or - 8 + c = 1c = 9 ,

and the equation of the line is

y = 4 x + 9 .

Example 5

Two lines are described as follows: the first has gradient-1 and passes through the point R(2,1) ; the second passes through thetwo points with coordinates P(2,0) and Q(0,4) . Find the equation ofboth lines and find the coordinates of their point of intersection.

Solution

The first line has gradient m = - 1 so it must be y =( - 1) x + c , i.e. y = - x + c , for some c . Since the line passes throughthe point R (2 , 1) these values of x, y must satisfy the equation. Thus2 = - (1)+ c so c = 3 . The first line therefore has equation y = - x +3 . For the second case both points lie on the line and so satisfy theequation. If the equation is y = mx + c then putting these values intothe equation gives

y = mx + c

0 = 2 m + c (using the coordinates of P )

4 = c (using the coordinates of Q )

These equations yield m = - 2 and c = 4 .

The second line thus has the equation y = - 2 x +4 . The equations of the two lines can now be rewritten as

y + x = 3 (1)

y + 2 x = 4 (2)

which is a pair of simultaneous equations. Subtracting equation (1) from equation (2) gives x = 1 and substituting this into the first equationthen yields y = 2 . The point of intersection thus has coordinates x = 1 , y = 2 . (By substituting these coordinates into equation (2) and verifying that they satisfy the equation, it can be checked that this is also a point on the second line.)

Some Useful Facts

• Parallel lines have the same gradient. Thus, for example, the lines with equations y = 3 x + 7 andy = 3 x - 2 are parallel.

• Lines parallel to the x -axis have equations of the form y = k, for some constant, k .

• Lines parallel to the y -axis (when m = 0 ) have equations of the form x = k , for some constant, k .

• The larger the absolute value of m , the ‘steeper’ the slope of the line.

• If two lines intersect at right angles then the product of their gradients is - 1 . The lines y = - 7 x +4and y = (1 / 7) x + 5 , for example, intersect each other at right angles.