Solving Quadratic Inequalities with a Sign Graph
An inequality involving a quadratic polynomial is called a quadratic inequality.
Quadratic Inequality
A quadratic inequality is an inequality of the form
ax2 + bx + c > 0, where a, b, and c are real numbers with a
≠ 0. The inequality symbols <,
≤, and ≥ may also be used.
If we can factor a quadratic inequality, then the inequality can be solved with a
sign
graph, which shows where each factor is positive, negative, or zero.
Example 1
Solving a quadratic inequality
Use a sign graph to solve the inequality x2 + 3x - 10 > 0.
Solution
Because the left-hand side can be factored, we can write the inequality as
(x + 5)(x - 2) > 0.
This inequality says that the product of x + 5 and x - 2 is positive. If both factors
are negative or both are positive, the product is positive. To analyze the signs of
each factor, we make a sign graph as follows. First consider the possible values of
the factor x + 5:
| Value |
Where |
On the number line |
| x + 5 = 0 x + 5 > 0
x + 5 < 0 |
if x = -5 if x > -5
if x < -5 |
Put a 0 above -5. Put + signs to the right of -5.
Put - signs to the left of -5. |
The sign graph shown in the figure below for the factor x + 5 is made from the information
in the preceding table.
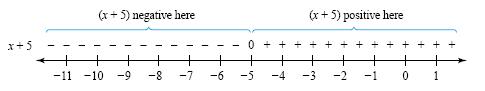
Now consider the possible values of the factor x - 2:
| Value |
Where |
On the number line |
| x - 2 = 0 x - 2 > 0
x - 2 < 0 |
if x = 2 if x > 2
if x < 2 |
Put a 0 above 2. Put + signs to the right of 2.
Put - signs to the left of 2. |
We put the information for the factor x - 2 on the sign graph for the factor x
+ 5
as shown in the figure below.
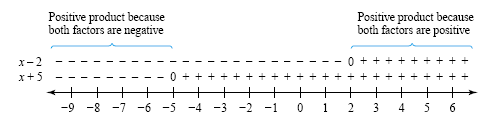
We can see from this figure that the product is positive if
x < -5 and the product is positive if x >2. The solution set for the quadratic
inequality is shown in the next figure.
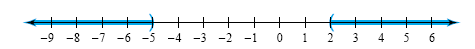
Note that -5 and 2 are not included in the graph because
for those values of x the product is zero. The solution set is (-∞�,-5)
È (2, ∞).
In the next example we will make the procedure from Example 1 a bit more
efficient.
Example 2
Solving a quadratic inequality
Solve 2x2 + 5x
≤ 3 and graph the solution set.
Solution
Rewrite the inequality with 0 on one side:
| 2x2 + 5x - 3 |
≤ 0 |
|
| (2x - 1)(x + 3) |
≤ 0 |
Factor |
Examine the signs of each factor:
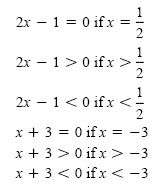
Make a sign graph as shown in the figure below.
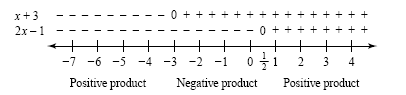
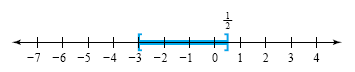
The product of the factors is negative between -3 and
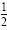 , when one factor is negative and the other is positive. The product
is 0 at -3 and at , when one factor is negative and the other is positive. The product
is 0 at -3 and at
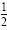 . So the solution set is the interval . So the solution set is the interval
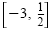 . The graph of the
solution set is shown in the following figure. . The graph of the
solution set is shown in the following figure.
|