| Background
The graph of a quadratic expression has a U-shaped graph called a
parabola. We can write a quadratic expression in the form ax2
+ c, where a is called the leading
coefficient. The way the parabola opens depends on the sign of the leading
coefficient. In fact, if a is positive, the parabola opens up; if a is negative, the parabola opens down. If the
absolute value of a is greater than 1, then the
parabola is narrower than y = x2. If the absolute
value of a is less than 1, then the parabola is wider
than y = x2.
A quadratic function can be written in different
forms. Each form gives information about the graph.
Standard Form (no linear term) |
Warm-Up
y = -3x2 + 4 matches
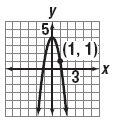 . .
“This quadratic function is written in standard form.
Because the leading coefficient is negative, the
graph opens down. The 3 causes the graph to be
narrower than y = x2. The vertex is at (0, 4),
because the graph has been shifted upward 4 units.
You can test the ordered pair (1, 1). When x = 1, y = -3(1)2 + 4,
which is 1.â€
|
| y = ax2 + c |
Graphical Information
c > 0:
vertical shift
upward of c units
c < 0:
vertical shift
downward of
c units |
Warm-Up
y = (x + 3)2 + 1 matches
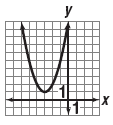 . .
“This quadratic function can be written in vertex
form as The vertex is at
The graph opens up because a is positive.â€
|
| y = a(x - h)2 + k |
Graphical Information vertex at
(h, k) |
Warm-Up
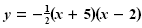 matches matches
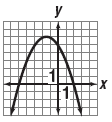 .
“This quadratic function is written in factored form.
The graph opens down because a is less than 0.
Because .
“This quadratic function is written in factored form.
The graph opens down because a is less than 0.
Because
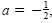 the graph is wider than
y = x2.
The intercepts are at (-5, 0) and (2, 0)†the graph is wider than
y = x2.
The intercepts are at (-5, 0) and (2, 0)â€
|