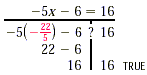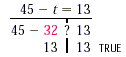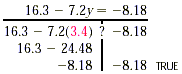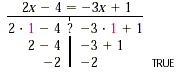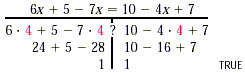|
|
Solving EquationsMost of algebra involves either simplifying expressions (by writing equivalent expressions) or solving equations (by writing equivalent equations). We can use the addition and multiplication principles to produce equivalent equations, like x = 5 from which the solution - in this case, 5- is obvious. Here we will find that more complicated equations can be solved by using both principles together and by using the commutative, associative, and distributive laws to write equivalent expressions. An important strategy for solving a new look like a problem we already know how to solve. This is precisely the approach taken in this section. What is new in this section appears in the early steps of each example. Without a solid grasp of how and when to use the addition and multiplication principles, the problems in this section will seem much more difficult than they really are. Using both the Addition and Multiplication PrinciplesIn the expression 5 + 3x the variable x is multiplied by 3 and then 5 is added. To reverse these steps, we first subtract 5 and then divide by 3. Thus, to solve 5 + 3x = 17 we first subtract 5 from each side and then divide both sides by 3. Example 1 Solve: 5 + 3x = 17 Solution We have 5 + 3x = 17 5 + 3x - 5 = 17 - 5 Using the addition principle: subtracting 5 from both sides (adding -5) 5 + (- 5) + 3x = 12 Using a commutative law. Try to perform this step mentally. First isolate the x-term 3x = 12 Simplifying
Then isolate x x = 4 Simplifying Check:
The solution is 4. Multiplication by a negative number and subtraction are handled in much the same way. Example 2 Solve -5x -6 = 16. Solution In -5x -6 we multiply first and then subtract. To reverse these steps, we first add 6 and then divide by -5. -5x -6 = 16 -5x -6 + 6 = 16 + 6 Adding 6 to both sides.
Check:
The soultion is Example 3 Solve 45 - t = 13. Solution 45 - t = 13 45 - t - 45 = 13 - 45 Substracting 45 from both sides.
-t = -32 Try to go directly to this step (-1)(-t) = (-1)(-32) Multiply both sides by -1 (Dividing by -1 would also work) t = 32 Check:
The soultion is 32. As our skills improve, many of the steps can be streamlined. Example 4 Solve 16.3 - 7.2y = -8.18 Solution We have 16.3 - 7.2y = -8.18 - 7.2y = -8.18 -16.3 Subtracting 16.3 from both sides. We write the subtraction of 16.3 on the right side and remove 16.3 from the left side. - 7.2y = -24.48
y = 3.4 Check:
The solution is 3.4. Combining Like TermsIf like terms appear on the same side of an equation, we combine them and then solve. Should like terms appear on both sides of an equation, we can use the addition principle to rewrite all like terms on one side Example 5 Solve: a) 3x + 4x = -14 b) 2x - 4 = -3x + 1 c) 6x + 5 -7x = 10 - 4x + 7 d) 2 - 5(x + 5) = 3(x - 2) - 1 Solution a) 3x + 4x = -14 7x = -14 Combining like terms
x = -2 The check is left to the student. The solution is -2. To solve 2x - 4 = -3x + 1 we must first write only variable terms on one side and only constant terms on the other. This can be done by adding 4 to both sides, to get all constant terms on the right, and 3x to both sides, to get all variable terms on the left. We can add 4 first, or 3x first, or do both in one step. 2x - 4 = -3x + 1 2x - 4 + 4 = -3x + 1 + 4 Adding 4 to both sides 2x = -3x + 5 Simplifying 2x + 3x = -3x + 3x + 5 Adding 3x to both sides 5x = 5 Combining like terms and simplifying
x = 1 Simplifying Check:
The solution is 1. c) 6x + 5 - 7x = 10 - 4x + 7 -x + 5 = 17 - 4x Combining like terms on both sides -x + 5 + 4x = 17 - 4x + 4x Adding 4x to both sides 5 + 3x = 17 Simplifying. This is identical to Example 1 3x = 12 Subtracting 5 from both sides and simplifying x = 4 Dividing both sides by 3 and simplifying. Check:
The solution is 4. d) 2 - 5(x + 5) = 3(x - 2) - 1 2 - 5x - 25 = 3x - 6 - 1 Using the distributive law. This is now similar to part (c) above. -5x - 23 = 3x - 6 Combining like terms on both sides
-16 = 8x Simplifying -2 = x Dividing both sides by 8 The student can confirm that -2 checks and is the solution. |
|


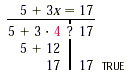 We use the rules for order of operations:
Find the product
We use the rules for order of operations:
Find the product