Multiplying and Dividing Fractions
Examples with Solutions
Example 1: Multiply 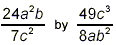
solution: This is just another way of posing the problem:
Simplify: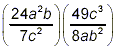
Proceeding as in the previous example, we get
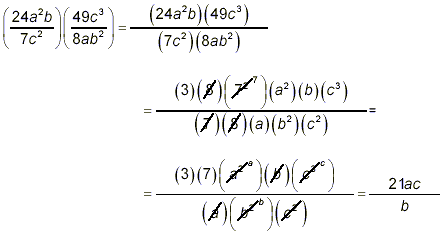
as the final solution. We could have done this last step as
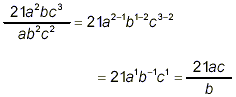
to get the same final result, once factors are repositioned
between the numerator and denominator to get rid of negative
exponents.
Example 2: Simplify 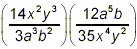 . .
solution: This is very similar to the expressions handled in
the first two examples. Proceeding in the same fashion, we get
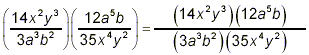 (This is what the actual multiplication
of the two fractions amounts to. Now this result must be
simplified.) (This is what the actual multiplication
of the two fractions amounts to. Now this result must be
simplified.)
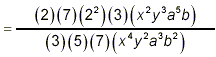 (Here we expand the numerical factors
into products of prime factors, and we also sort out the various
literal factors.) (Here we expand the numerical factors
into products of prime factors, and we also sort out the various
literal factors.)
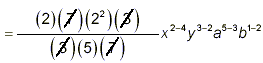 (Cancel the common numerical factors and
combine powers of the literal symbols.) (Cancel the common numerical factors and
combine powers of the literal symbols.)
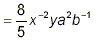 (This is a fully simplified form, but it
contains negative exponents.) (This is a fully simplified form, but it
contains negative exponents.)
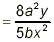
as the final result with negative exponents eliminated.
Example 3: Simplify 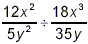 . .
solution: This is one fraction divided by another. Following
the pattern given at the beginning of this document, we know that
the first step here is to rewrite the expression as the first
fraction multiplied by the reciprocal of the second fraction:
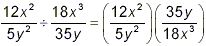
Now the remainder of the work is to simplify this
multiplication, exactly as we dealt with the first three
examples. So
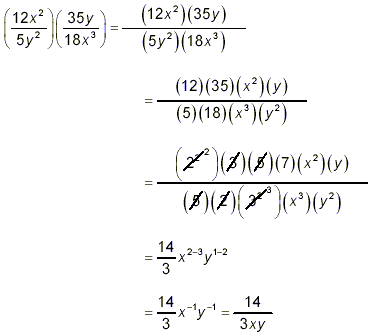
as the final answer.
A very common error here is to start by correctly rewriting
the original division problem as a multiplication, but then doing
the multiply step in a totally bizarre way – numerators with
denominators, as in
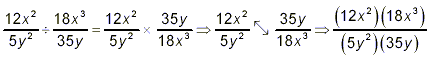
But this is totally wrong! When we multiply two fractions, it
is always numerator times numerator and denominator times
denominator, regardless of where the multiplication problem
originally came from. If you examine the eventual result that
would be obtained here, you’ll see that it amounts to what
we would get if we had multiplied the two original fractions
together, rather than dividing the first fraction by the second
one. In other words, what has effectively been done by using this
erroneous method is to change the original division symbol to a
multiplication symbol. This must be an error. So, always
remember: dividing by a fraction is equivalent to multiplying by
its reciprocal, and multiplying is always done the same way,
regardless of from where the original fractions were obtained.
|