Solving Quadratic Equations
Completing the Square
The Vertex Form of a Quadratic Function
The format for a quadratic equation given above,
y = a · x 2 + b
· x + c, where the letter x represents the input, the letter y represents the value of the output and
the letters a, b and c are all numbers, is called standard form.
Other ways of writing the equations for quadratic functions include vertex form,
y = a · (x - h) 2 + k,
where the letter x represents the value of the input, the letter y represents the value of the
output and the letters a, h and k all represent numbers. Just as in standard form, in vertex
form the number a cannot be equal to zero. Converting a quadratic equation to vertex
form is often quite helpful as it allows you to determine exactly where the graph of the
quadratic equation reaches its “low point†or “high point†very easily. Every single
quadratic formula can be converted to vertex form. The process for doing this conversion
is called completing the square.
What the Vertex Form of a Quadratic can tell you about the graph
The vertex form of a quadratic function:
y = a · (x - h) 2 + k,
also tells you whether the graph of the quadratic is smiling or frowning. To check,
simply look at the value of a, as you would if the equation had been written in standard
form. If the value of a is positive then the quadratic is smiling and if the value of a is
negative then the quadratic will be frowning.
The vertex form of a quadratic equation can also tell you about the location of the highest
point (on a frowning quadratic) or the lowest point (on a smiling quadratic – see Figure 1
on the next page). This point (the highest point on a frowning quadratic or the lowest
point on a smiling quadratic) is called the vertex.
The x-coordinate of the vertex is the number h that appears inside the parentheses of the
vertex form and the y-coordinate of the vertex is the number k that appears outside the
parentheses in the vertex form.
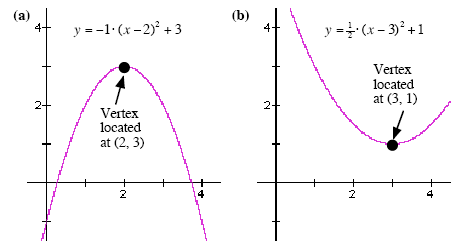
Figure 1: (a) In this quadratic, a = -1 and the shape of the graph is a “frown.†The vertex
in this case is the highest point on the graph. (b) In this quadratic a = 0.5 and the shape
of the graph is a “smile.†The vertex in this case is the lowest point on the graph.
|