Graph of a Line
We can graph the linear equation defined by y = x + 1 by
finding several ordered pairs. For example, if x = 2 then y = 2 +
1 = 3, giving the ordered pair (2, 3). Also, (0, 1), (4, 5), (-2,
-1), (-5, -4), (-3, -2), among many others, are ordered pairs
that satisfy the equation.
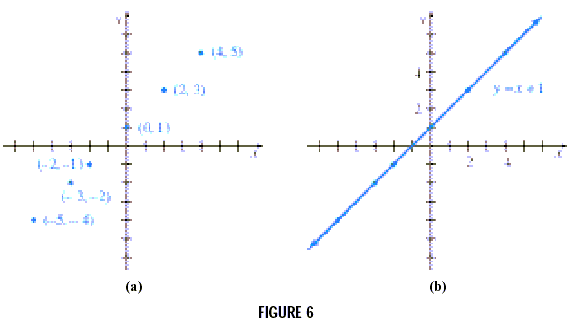
To graph y = x + 1 we begin by locating the ordered pairs
obtained above, as shown in Figure 6(a). All the points of this
graph appear to lie on a straight line, as in Figure 6(b). This
straight line is the graph of y = x + 1.
It can be shown that every equation of the form ax + by = c
has a straight line as its graph. Although just two points are
needed to determine a line, it is a good idea to plot a third
point as a check. It is often convenient to use the x- and
y-intercepts as the two points, as in the following example.
Example
Graph of a Line
Graph 3x + 2y = 12.
Solution
To find the y -intercept, let x = 0.
| 3(0) + 2y = 12 |
|
| 2y = 12 |
Divide both sides by 2. |
| y = 6 |
|
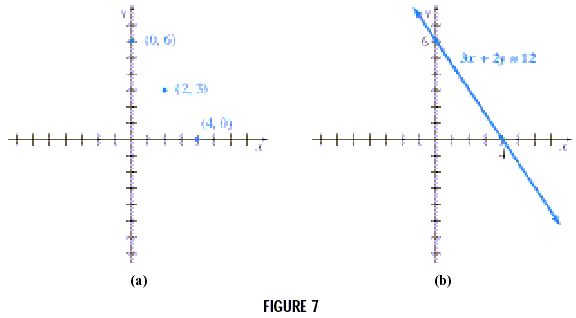
Similarly, find the x-intercept by letting y = 0 which gives x
= 4. Verify that when x = 2 the result is y = 3. These three
points are plotted in Figure 7(a). A line is drawn through them
in Figure 7(b).
Not every line has two distinct intercepts; the graph in the
next example does not cross the x-axis, and so it has no
x-intercept.
Example
Graph of a Horizontal Line
Graph y = -3.
Solution
The equation y = -3 or equivalently y = 0x -3, always gives
the same y -value, - 3, for any value of x . Therefore, no value
of x will make y = 0, so the graph has no x -intercept. The graph
of such an equation is a horizontal line parallel to the x -axis.
In this case the y -intercept is - 3, as shown in Figure 8.
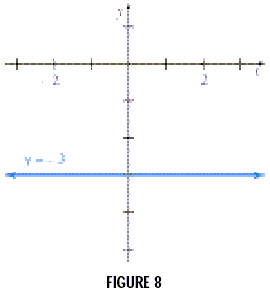
In general, the graph of y = k, where k is a real number, is
the horizontal line having y-intercept k.
The graph in Example 13 had only one intercept. Another type
of linear equation with coinciding intercepts is graphed in
Example 14.
Example
Graph of a Line Through the Origin
Graph y = -3x.
Solution
Begin by looking for the x -intercept. If y = 0 then
| y = -3x |
|
| 0 = -3x |
Let y = 0 |
| 0 = x |
Divide both sides by -3 |
We have the ordered pair (0, 0). Starting with x = 0 gives
exactly the same ordered pair, (0, 0). Two points are needed to
determine a straight line, and the intercepts have led to only
one point. To get a second point, choose some other value of x
(or y ). For example, if x = 2 then
y = -3x = -3(2) = -6, (let x = 2)
giving the ordered pair (2, -6). These two ordered pairs, (0,
0) and (2, -6), were used to get the graph shown in Figure 9.

|