Graphing Using x- and y- Intercepts
Once we know both the x-intercept and the y-intercept, we can
graph the equation.
Example 1
Graph 3x + 5y = 15 using the x- and y- intercept.
Solution
First, find the intercepts.
| To find the y -intercept, let
x = 0. |
To find the x-intercept, let
y = 0. |
| 3 · 0 + 5y |
= 15 |
3x + 5 · 0 |
= 15 |
| 5y |
= 15 |
3x |
= 15 |
| y |
= 3 |
x |
= 5 |
| The y-intercept is 3. |
The x-intercept is 5. |
| The ordered pair is (0, 3). |
The ordered pair is ( 5, 0) |
We now graph these two points and draw the line that contains
them.
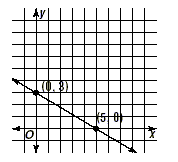
Slope-Intercept Form
The slope-intercept form is a special case of the point-slope
form, where the given point of the line (x 0 , y
0 ) lies on the y-axis, so x 0 = 0. This means
that the equation is of the form y - y 0 = mx, or y =
mx + y 0 . So, the equation is given explicitly when
we know both the intercept and the slope and it is simpler than
the more general point-slope form. This is the most common form
for the equation of a line.
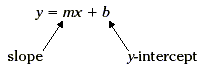
Key Idea An equation for a line is said to be
in slope-intercept form when it is of the form y = mx + b, where
m is the slope of the line and b is the y-coordinate of the
y-intercept. Any line that is not vertical has an equation that
can be written in slope-intercept form.
The equation of a vertical line cannot be written in
slope-intercept form because the slope of a vertical line is
undefined; that is, it has no slope.
|