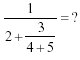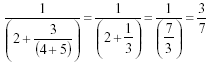Order of Operations

Look at “4 + 5 × 2”. How do you know which to do first? Should you add 4 plus 5 and then multiply by 2, or multiply first and then add?

Natural Order

There is a “natural” order of operations to mathematics:

1. If there’s any parentheses ( ) then do them first.

2. Then do exponents xⁿ and powers 10³ and radicals .

3. Then do multiplication × and division ÷.

4. And then do any addition + and subtraction - from left to right.

It may help to remember them as P.E.M.D.A.S. using their first letters.

Thus in the example 4 + 5 × 2, we would multiply first.

Example:

8 - 4 - 1 = ?

Answer:

Since we have more than one subtraction, we do the left one first:

(8 - 4) - 1 = 3

Parentheses

What if we wanted to tell someone to do the subtraction in a different order? Use parentheses to change the natural order. Expressions in parentheses are always done first. Note: Singular is parenthesis, and plural is parentheses.

Example:

8 - (4 - 3) = ?

Answer:

The parentheses tell us to do “four minus one” first:

8 - (4 - 3) = 7

What about nested parentheses? Evaluate the innermost parentheses first.

Example:

( 8 - (4 + 2))² = ?

Answer:

( 8 - 6)² = (2)² = 4

Exponents

Suppose you have an expression with both subtraction and exponents. You should do the exponent first (unless commanded otherwise by parentheses).

Example:

25 - 2⁴ = ?

Answer:

Since there is no parentheses ( ) we do “two to the fourth power” first: 25 - 16 = 9

Calculator Warning!

See your calculator’s manual to read about its order of operations. The cheapest ones simply do everything left-to-right as you enter the operations. The better ones save the results of multiplication and then add (or subtract) the products together. Try this on your calculator:

2 ×3 + 4 × 5 = ?

A very basic calculator solves it like this, as you enter it from left-to-right:

2 × 3 + 4 × 5

6 + 4 × 5

10 × 5 

50

A better calculator will follow the natural order of operations, and give a different answer even though you pressed the same keys in the same order:

2 × 3 + 4 × 5

6 + 4 × 5

6 + 20

26

So be sure to understand how your own calculator handles its order of operations!

By the way, most calculators that follow the natural order (multiplication first) also have parentheses keys so you can change the order, if needed. If you see parentheses on a calculator, that’s a good clue that it was designed to handle the natural order of operations. If in doubt, use the parentheses keys “(“ and “)” to ensure it follows the order you want.

More Examples

If a = 4 and b = 3 compute the result:

Example 1:

a + 6 - b = ?

Answer:

Add and subtract from left to right: 4 + 6 - 3 = 7

Example 2:

a / 2 × b = ?

Answer:

Multiply and divide from left to right: 4 / 2 × 3 = 6

Example 3:

b - a / 2 = ?

Answer:

The division comes first, then the subtraction: 3 - 4 / 2 = 1

Handling Fractions

One last complication: What about the expression

To figure this out, we must tell you there are always implied parentheses around the numerator and denominator of a fraction. So first do addition and subtraction, and then do the division:

What about cascading fractions such as ? This can be either or which give different results. The writer must be clear when putting it on paper! This is another great reason to love parentheses.

Example:

Answer:

Use the implied parentheses around each fraction, then start with the innermost and work your way out.